
Let’s understand more about this geometric shape which is present at almost all sites in our vicinity.Ī triangle is a three-sided and two-dimensional closed structure. From the sandwiches you eat in breakfast, high-level geometrical calculations you do in school to the dangerous Bermuda triangle, almost everything is triangular. One might have often come across different foods or things which are triangular in shape. The bed, glass, mirror, laptop, oven, and other items of daily use have distinct geometrical shapes. Medians are used in geometry to help define the shape of a triangle and to calculate properties like perimeter and area.Aren’t most of us fascinated with geometrical shapes? One comes across an array of geometrical shapes in day-to-day life.

The median of a triangle is a line segment that connects a vertex of the triangle to the midpoint of the opposite side. That’s how you find the median of a triangle! Once you have that information, you can use the following equation:Median = (side1 + side2 + side3)/2For example, if you have a triangle with sides that are 3, 4, and 5 feet long, you would plug those numbers into the equation like this:Median = (3 + 4 + 5)/2Median = 12/2Median = 6 feet To find the median of a triangle, you need to know the lengths of all three sides of the triangle. Be sure to practice calculating medians using both proportions and algebra so that you are comfortable with both methods!įAQ What is the equation to find the median of a triangle? Medians can be used to find heights and identify similar triangles. The median is an important concept in geometry that has many real-world applications. M is midway between B and C implies MB + MC = 2*AM 6 + MC = 2*4 MC = 8 - 6 MC = 2 therefore median MN = 2 units To do this, set up two equations using information given in your question and then solve for x using any method you wish (substitution or elimination). See below for an example:ĪC/MN = AM/x AM = AC*x/MN x = AM*MN/AC median MN = x = 6*6/9 = 4Īlgebra Method: You can also use algebra to calculate medians. This value x will represent half of your desired median. Once you have found two similar triangles, set up a proportion equation and solve for x. Proportions Method: To use proportions, you will need to find two similar triangles-triangles that have corresponding angles with equal measures and/or sides with equal proportions. We will briefly explore both methods below.

There are two ways to calculate medians: using proportions or using algebra. The height can also be thought of as the length of the median extended past its point of intersection with the base. The height of a triangle is the perpendicular distance from the base (side) to the apex (vertex).
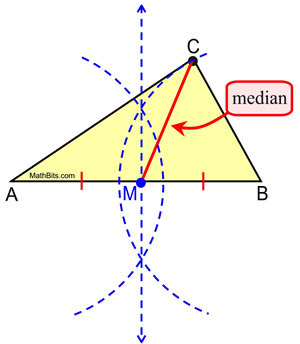
Medians are important because they can be used to find the height of a triangle. In the triangle above, we can see that there are three medians: MN, which joins vertex M to the midpoint of side BC PQ, which joins vertex P to the midpoint of side AC and RS, which joins vertex R to the midpoint of side AB. In other words, it is the line drawn from a corner of a triangle to the midpoint of the side opposite that corner.

#Median geometry in real life how to
In this blog post, we will explore what medians are, why they are important, and how to calculate them.Ī median is a line segment joining a vertex of the triangle to the midpoint of the opposite side. In geometry, a median of a triangle is a line segment joining a vertex of the triangle to the midpoint of the opposite side.


 0 kommentar(er)
0 kommentar(er)
